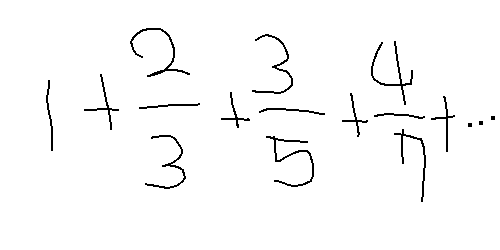数学自信ニキ来てくれ

**名無しなのに合格** · 2019/02/05(火) 22:49:19.38

この無限級数は発散する？収束する？
1＋2/3＋3/5＋4/7······

**名無しなのに合格** · 2019/02/05(火) 22:50:13.60

すまん文字化けは･･･や

**名無しなのに合格** · 2019/02/05(火) 22:56:19.14

第n項がn/2n-1だからn→∞のとき1/2になって発散じゃない？

**名無しなのに合格** · 2019/02/05(火) 22:56:48.80

これの無限級数が発散するか収束するか教えて欲しい

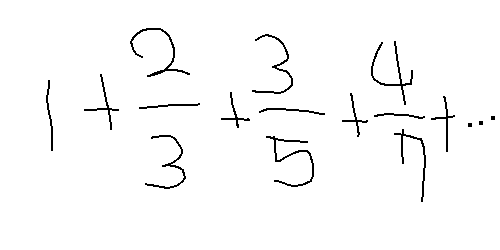
**名無しなのに合格** · 2019/02/05(火) 23:00:59.87

1/2になるのに発散するの？
どういうことや？

**名無しなのに合格** · 2019/02/05(火) 23:02:04.37

すまん分かったわ
級数は和やったわ
勘違いしてたわ

**名無しなのに合格** · 2019/02/05(火) 23:05:58.09

項をan、和をSnと置くと
an=Sn-S(n-1)だから、和が収束するのならn→∞のときSn-S(n-1)=0にならなきゃいけない
だからn→∞でan≠0ならその級数が発散すると言える

**名無しなのに合格** · 2019/02/05(火) 23:08:54.27

>>7
ありがとう

**名無しなのに合格** · 2019/02/05(火) 23:09:40.69

じゃあ君に追加問題をあげよう

**名無しなのに合格** · 2019/02/05(火) 23:10:37.70

**名無しなのに合格** · 2019/02/05(火) 23:11:52.22

ダランベールの判定法使わなきゃいけない

**名無しなのに合格** · 2019/02/05(火) 23:11:54.94

下の調和級数の発散を示せ

**名無しなのに合格** · 2019/02/05(火) 23:19:30.03

>>9
どっちも０

**名無しなのに合格** · 2019/02/05(火) 23:34:46.90

log2,π/4,log2/2,logxの区分求積
ちなみに最後以外は少なくとも入試レベルではない(高校数学で示せるが)

**名無しなのに合格** · 2019/02/05(火) 23:36:07.64

>>13
違うよ
証明はググってもいいし自分で解いてもいい
ヒントは
fn(x)=1/(x+1)-Σ[k=1,n](-x)^(k-1)として
∫fn(x)dx ∫fn(x^2)dx ∫xfn(x^2)dxを計算

**名無しなのに合格** · 2019/02/05(火) 23:37:46.92

>>14
区分求積なの？
入試レベルではないって何だ？
入試問題に普通にあるよ

**名無しなのに合格** · 2019/02/05(火) 23:40:47.36

1/xの積分と区分求積ではさむんやlogじゃない
誘導めちゃめちゃしてやろ?特にライプニッツ級数なんか日本女子大の自己推薦かなんかの
めっちゃ試験時間長い奴であったはずやで

**名無しなのに合格** · 2019/02/05(火) 23:41:06.05

>>9,10を誘導なしで解けるのは知ってるやつだけだろう
入試問題で出すにはセンスがない

**名無しなのに合格** · 2019/02/05(火) 23:42:02.05

12はやったことあるけど9.10は初見で何で挟めばいいか出なかったわ

**名無しなのに合格** · 2019/02/05(火) 23:42:51.33

>>17
誘導は確かにあったけど
その誘導含めて全部の証明覚えたわ
証明ラクだし
>>15だけで余裕で証明できるよ

**名無しなのに合格** · 2019/02/05(火) 23:44:35.95

数学が好きで交換級数の美しさに見とれて証明を覚えてしまった。

**名無しなのに合格** · 2019/02/05(火) 23:46:20.31

微積分/基礎の極意っていう本の演習問題にあった
北大の問題らしい

**名無しなのに合格** · 2019/02/05(火) 23:46:55.43

どこで聞けばいいかわからんからここで質問させてもらうけど
大学入試においてチェバの定理の逆、メネラウスの定理の逆って証明無しに使っていいもの？

**名無しなのに合格** · 2019/02/06(水) 00:20:48.90

どうしたの？答えられないの？
なら……答えられるようにしてあげるわ！！！

**名無しなのに合格** · 2019/02/06(水) 17:18:41.36

>>23
国立大の数学の教授と雑談した時にロピタルの定理を証明無しに使っても丸にしますかって聞いたら
正しく使われてるなら正解として扱うと迷う事なく答えてた
だから大丈夫だろう